[Contourner le dépassement de mémoire]
jesuiszero2
Messages postés
2
Date d'inscription
Statut
Membre
Dernière intervention
-
jesuiszero2 Messages postés 2 Date d'inscription Statut Membre Dernière intervention -
jesuiszero2 Messages postés 2 Date d'inscription Statut Membre Dernière intervention -
Bonjour la mifa,
Me Voici enfin dans la communauté,
Chers ingénieurs, depuis 3 mois, je bosse sur l'algorithme me permettra de parcourir et traiter les arbres binaires, mais ... vrai vrai là je suis fatigué. J'ai tout fais en vain.Mais ma conscience me dit qu'il doit nécessairement exister une méthode ou une manière de le faire.
Voici mon problème mes gares:
D'abord primo, ce n'est pas un exercice, c'est un projet perso que je doit valider (une sorte d'un défi dans mon entreprise).
Secondo, je vais essayer de m'expliquer aussi mieux pour être plus clair.
Tertio, je suis débutant dans le traitement des arbres binaires et qu'après mes recherches et analyse des différentes méthodes de parcours des arbres, j'ai finalement opter la méthode ci-dessous pour mon problème.
Mon algo consiste à retrouver le numéro d'un élément de l'arbre à une grande profondeur(le défi ici est de réduire le numéro de cet élément à cette profondeur aussi petite que possible c'est à dire pas question de traiter les nombres à millions de chiffre) et d'appliquer la méthode de parité pour descendre jusqu'à la racine.
En analysant l'arbre ci-dessus et par construction, on peut dire : il y a 2^n ascendants au degré n.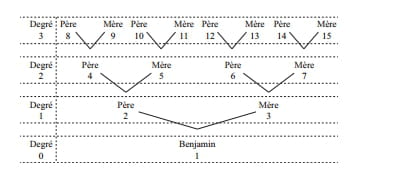
Par construction de l'arbre, à partir du degré 1 (racine), les pères ont un numéro pair et les mères un numéros impair.
par construction, le numéro de tout ascendant est 2p.
De façon général, si p est pair, le descendant porte le numero p/2, et si p est impair, le descendant porte le numero (p-1)/2
Dans mes recherches j'aurais appris qu'on peut retrouver le chemins d'un ascendants( élément de l'arbre) en connaissant sa position(son numero).
Exemple le degré 9 comporte 512 ascendants (2^9). Si on se positionne sur l'ascendant portant le numéro 612. on peut parcourir le chemin suivant:
Voici mes limites dans mon algo.
Je doit traiter les données au degré n=8388608 donc j'ai affaire à 2^8388608 ascendants au degré 8388608 portant donc des numéros aussi grand.
Question:
- Comment traiter ses données aussi grand facilement ( existe-t-il une astuce de transformer ces nombres en des valeurs plus petites) ?
- Existe-t-il des formules mathématiques plus simples pour la résolution ?
PS : Vos explications, astuces, formules mathématiques, algo me fairons plaisir.
Esperant vous avoir mieux expliquer mon problèmes, je suis à vous la communauté !!!!
Me Voici enfin dans la communauté,
Chers ingénieurs, depuis 3 mois, je bosse sur l'algorithme me permettra de parcourir et traiter les arbres binaires, mais ... vrai vrai là je suis fatigué. J'ai tout fais en vain.Mais ma conscience me dit qu'il doit nécessairement exister une méthode ou une manière de le faire.
Voici mon problème mes gares:
D'abord primo, ce n'est pas un exercice, c'est un projet perso que je doit valider (une sorte d'un défi dans mon entreprise).
Secondo, je vais essayer de m'expliquer aussi mieux pour être plus clair.
Tertio, je suis débutant dans le traitement des arbres binaires et qu'après mes recherches et analyse des différentes méthodes de parcours des arbres, j'ai finalement opter la méthode ci-dessous pour mon problème.
Mon algo consiste à retrouver le numéro d'un élément de l'arbre à une grande profondeur(le défi ici est de réduire le numéro de cet élément à cette profondeur aussi petite que possible c'est à dire pas question de traiter les nombres à millions de chiffre) et d'appliquer la méthode de parité pour descendre jusqu'à la racine.
En analysant l'arbre ci-dessus et par construction, on peut dire : il y a 2^n ascendants au degré n.
Par construction de l'arbre, à partir du degré 1 (racine), les pères ont un numéro pair et les mères un numéros impair.
par construction, le numéro de tout ascendant est 2p.
De façon général, si p est pair, le descendant porte le numero p/2, et si p est impair, le descendant porte le numero (p-1)/2
Dans mes recherches j'aurais appris qu'on peut retrouver le chemins d'un ascendants( élément de l'arbre) en connaissant sa position(son numero).
Exemple le degré 9 comporte 512 ascendants (2^9). Si on se positionne sur l'ascendant portant le numéro 612. on peut parcourir le chemin suivant:
Voici mes limites dans mon algo.
Je doit traiter les données au degré n=8388608 donc j'ai affaire à 2^8388608 ascendants au degré 8388608 portant donc des numéros aussi grand.
Question:
- Comment traiter ses données aussi grand facilement ( existe-t-il une astuce de transformer ces nombres en des valeurs plus petites) ?
- Existe-t-il des formules mathématiques plus simples pour la résolution ?
PS : Vos explications, astuces, formules mathématiques, algo me fairons plaisir.
Esperant vous avoir mieux expliquer mon problèmes, je suis à vous la communauté !!!!
A voir également:
- [Contourner le dépassement de mémoire]
- Mémoire vive - Guide
- RAM : type, format, CAS, vitesse, tout sur la mémoire vive - Guide
- Le logiciel amd a détecté un dépassement de délai du pilote - Forum Processeur
- Mémoire validée ✓ - Forum Windows 10
- Le logiciel amd a détecté un dépassement de délai du pilote ✓ - Forum Carte graphique
2 réponses
Bonjour
C'est pas parce que tu dis que ça n'est pas un exercice que l'on fera le travail à ta place, si cela fait si longtemps que tu travailles dessous tu doit être en mesure de montrer que ce tu as essayé et de préciser où apparaît ton problème, qui selon ton titre est un dépassement de capacité et selon ton texte on ne sait pas trop....
Je suppose que si tu as un dépassement de capacité, c'est donc que ton algo, tu l'as écrit dans un langage quelconque, que tu n'as pas précisé, cela aurait utile, non?
C'est pas parce que tu dis que ça n'est pas un exercice que l'on fera le travail à ta place, si cela fait si longtemps que tu travailles dessous tu doit être en mesure de montrer que ce tu as essayé et de préciser où apparaît ton problème, qui selon ton titre est un dépassement de capacité et selon ton texte on ne sait pas trop....
Je suppose que si tu as un dépassement de capacité, c'est donc que ton algo, tu l'as écrit dans un langage quelconque, que tu n'as pas précisé, cela aurait utile, non?
Au fait, il s'agit de trouver le numéro d'un élément au degré n. Cela j'arrive à le prouver théoriquement.
Avec des données plus petites de l’élément E dans l'arbre (degré n <= 23), cela est possible aussi théorique que pratique.
Ici le seul souci est que ce nombre devient trop grand au degré n supérieur ( n > 2^32) puisque à ce degré on a affaire à (2^8388608+1)-1 nœuds. ce qui donne des grands nombres à quelques millions de chiffres.
J'ai manipuler les BigInteger en java et même voir du côté de python.
Or mon boulot consiste à permettre que le système A calcule la position de l'élément E de l'arbre connaissant évidemment le chemin pour atteindre E et ensuite envoie cette position au système B via GSM( maxi 160 caractères). Le système B doit être capable de retrouver le chemin en analysant bien sûr le numéro de l’élément E reçu.
voilà, c'est tout mon système !!!! qui m'arrache les cheveux.
Si nous prenons comme exemple l'arbre cité dans le post :
Le système A après calcul doit envoyer 612 comme position de l’élément au Système B. Le système B doit à son tour analyser le nombre 612 reçu et retrouver le chemin à parcours dans son arbre.
Pour faire simple c'est comme les système A envoie au système B un nombre qu'il doit analyser pour retrouver le chemin à parcourir (001100100 soit 6 zéro et 3 un, 6 hommes et 3 femmes).
NB : Système A et Système B sont indépendants
Avec des données plus petites de l’élément E dans l'arbre (degré n <= 23), cela est possible aussi théorique que pratique.
Ici le seul souci est que ce nombre devient trop grand au degré n supérieur ( n > 2^32) puisque à ce degré on a affaire à (2^8388608+1)-1 nœuds. ce qui donne des grands nombres à quelques millions de chiffres.
J'ai manipuler les BigInteger en java et même voir du côté de python.
Or mon boulot consiste à permettre que le système A calcule la position de l'élément E de l'arbre connaissant évidemment le chemin pour atteindre E et ensuite envoie cette position au système B via GSM( maxi 160 caractères). Le système B doit être capable de retrouver le chemin en analysant bien sûr le numéro de l’élément E reçu.
voilà, c'est tout mon système !!!! qui m'arrache les cheveux.
Si nous prenons comme exemple l'arbre cité dans le post :
Le système A après calcul doit envoyer 612 comme position de l’élément au Système B. Le système B doit à son tour analyser le nombre 612 reçu et retrouver le chemin à parcours dans son arbre.
Pour faire simple c'est comme les système A envoie au système B un nombre qu'il doit analyser pour retrouver le chemin à parcourir (001100100 soit 6 zéro et 3 un, 6 hommes et 3 femmes).
NB : Système A et Système B sont indépendants