Figure de Van Koch avec les nombres complexes
HubleFST
Messages postés
1
Statut
Membre
-
yg_be Messages postés 23541 Date d'inscription Statut Contributeur Dernière intervention -
yg_be Messages postés 23541 Date d'inscription Statut Contributeur Dernière intervention -
Bonjour,
Je m'adresse à vous car je bloque. Comme l'indique mon titre j'essaye de reproduire le flocon de Von Koch avec les nombres complexes, pour cela j'ai créé une fonction qui prend en argument 2 complexes A et B et qui retourne 5 points A B C D E avec C qui vaut 1/3 de AB, E qui vaut 2/3 de AB et D qui est le sommet du triangle équilatéral CED. Mon principal problème je pense viens du points D, lorsque je lance la fonction avec un même imaginaire pour A et B cela fonctionne (image 1) mais dans le cas contraire D se forme sans tenir compte de l'inclinaison de la droite (image 2). Si quelqu'un a une piste je suis preneur !
mon programme:
def TSC(A=complex(0,0),B=complex(1,0)):
distanceAB= B.real-A.real
C=complex(A.real+(1/3)*distanceAB,A.imag+(1/3*(B.imag-A.imag)))
E=complex(A.real+(2/3)*distanceAB,A.imag+(2/3*(B.imag-A.imag)))
distanceCE= E.real-C.real
D=complex(A.real+((distanceAB)*1/2),C.imag+((B.imag-A.imag)*1/2)+(C.real**2)-(((1/2)*distanceCE)**2)**1/2)
L=np.array([A,C,D,E,B])
X=np.real(L)
Y=np.imag(L)
pl.plot(X,Y)
pl.show()
return(A,C,D,E,B)
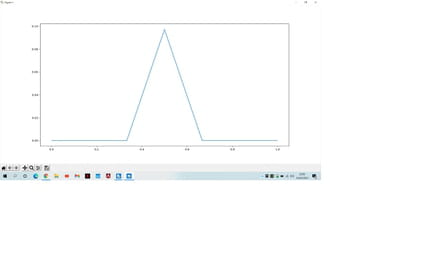
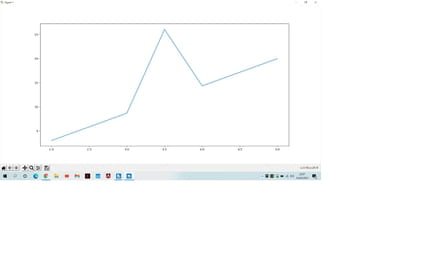
Je m'adresse à vous car je bloque. Comme l'indique mon titre j'essaye de reproduire le flocon de Von Koch avec les nombres complexes, pour cela j'ai créé une fonction qui prend en argument 2 complexes A et B et qui retourne 5 points A B C D E avec C qui vaut 1/3 de AB, E qui vaut 2/3 de AB et D qui est le sommet du triangle équilatéral CED. Mon principal problème je pense viens du points D, lorsque je lance la fonction avec un même imaginaire pour A et B cela fonctionne (image 1) mais dans le cas contraire D se forme sans tenir compte de l'inclinaison de la droite (image 2). Si quelqu'un a une piste je suis preneur !
mon programme:
def TSC(A=complex(0,0),B=complex(1,0)):
distanceAB= B.real-A.real
C=complex(A.real+(1/3)*distanceAB,A.imag+(1/3*(B.imag-A.imag)))
E=complex(A.real+(2/3)*distanceAB,A.imag+(2/3*(B.imag-A.imag)))
distanceCE= E.real-C.real
D=complex(A.real+((distanceAB)*1/2),C.imag+((B.imag-A.imag)*1/2)+(C.real**2)-(((1/2)*distanceCE)**2)**1/2)
L=np.array([A,C,D,E,B])
X=np.real(L)
Y=np.imag(L)
pl.plot(X,Y)
pl.show()
return(A,C,D,E,B)


A voir également:
- Figure de Van Koch avec les nombres complexes
- Van basco - Télécharger - DJ & Karaoké
- Nombre de jours entre deux dates excel - Guide
- Code binaire des nombres - Guide
- Nombres faciles - Télécharger - Outils professionnels
- Formule excel écart entre deux nombres - Forum Excel
1 réponse

yg_be
Messages postés
23541
Date d'inscription
Statut
Contributeur
Dernière intervention
Ambassadeur
1 586
bonjour,
ce n'est pas un problème de programmation, c'est un problème de géométrie.
https://www.commentcamarche.net/infos/25899-demander-de-l-aide-pour-vos-exercices-sur-ccm/
ce n'est pas un problème de programmation, c'est un problème de géométrie.
https://www.commentcamarche.net/infos/25899-demander-de-l-aide-pour-vos-exercices-sur-ccm/

