Calculatrice, présicion arbitraire ?
Résolu
Escienca
Messages postés
429
Date d'inscription
Statut
Membre
Dernière intervention
-
Escienca Messages postés 429 Date d'inscription Statut Membre Dernière intervention -
Escienca Messages postés 429 Date d'inscription Statut Membre Dernière intervention -
Bonjour,
Je voudrais savoir exactement ce que signifie "précision arbitraire" concernant les calculatrices ?
Pourquoi avec différentes calculatrices je trouve des résultats très différents, et très éloignés les un des autres ?
Par exemple:
Je calcule des inégalités triangulaires de Minkowski:
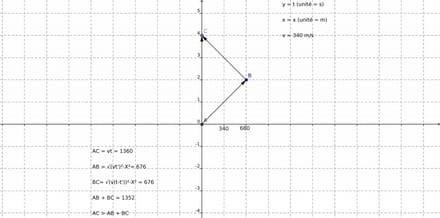
Avec le Calcotron, je trouve 676
Avec SpeedCrunch je trouve exactement 679,99705881716870849479 !!!
Donc voilà, si quelqu'un pouvait m'expliquer, svp, ces énormes différences de résultats finaux, je lui en serait gréé ! Merci
https://media4.obspm.fr/outils/calcotron/
SpeedCrunch est dans les sources Linux
Je voudrais savoir exactement ce que signifie "précision arbitraire" concernant les calculatrices ?
Pourquoi avec différentes calculatrices je trouve des résultats très différents, et très éloignés les un des autres ?
Par exemple:
Je calcule des inégalités triangulaires de Minkowski:
Avec le Calcotron, je trouve 676
Avec SpeedCrunch je trouve exactement 679,99705881716870849479 !!!
Donc voilà, si quelqu'un pouvait m'expliquer, svp, ces énormes différences de résultats finaux, je lui en serait gréé ! Merci
https://media4.obspm.fr/outils/calcotron/
SpeedCrunch est dans les sources Linux
A voir également:
- Calculatrice, présicion arbitraire ?
- Calculatrice gratuit - Télécharger - Calcul & Conversion
- Installation calculatrice - Télécharger - Calcul & Conversion
- Ma-calculatrice - Télécharger - Calcul & Conversion
- Calculatrice windows 7 - Télécharger - Calcul & Conversion
- Calculatrice disparue samsung - Forum Samsung
3 réponses
Les différences de résultats sont certainement dus à la précision interne de la calculatrice. A force d'approximation, on tombe sur ces écarts-là.
Bonjour,
Peu importe la calculatrice que tu auras, si tu fais 1/3 tu auras un résultat plus ou moins égal à 0.333333333 et en multipliant ce résultat par 3 tu obtiendras 0.999999999 au lieu d'avoir 1. C'est à cause de l'approximation.
Le seul moyen d'avoir le résultat exact c'est de faire du calcul formel.
Dans ce cas au lieu de manipuler les résultats au fur et à mesure et accumuler les erreurs d'approximations, on manipule des symboles ce qui fait que le résultat est toujours exact, jusqu'au résultat final.
Exemple d'identitié impossible à obtenir avec une évaluation numérique :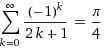
Exemple de résolution : sum((-1)^k/(2k+1),k,0,infinity)
Peu importe la calculatrice que tu auras, si tu fais 1/3 tu auras un résultat plus ou moins égal à 0.333333333 et en multipliant ce résultat par 3 tu obtiendras 0.999999999 au lieu d'avoir 1. C'est à cause de l'approximation.
Le seul moyen d'avoir le résultat exact c'est de faire du calcul formel.
Dans ce cas au lieu de manipuler les résultats au fur et à mesure et accumuler les erreurs d'approximations, on manipule des symboles ce qui fait que le résultat est toujours exact, jusqu'au résultat final.
Exemple d'identitié impossible à obtenir avec une évaluation numérique :
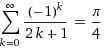
Exemple de résolution : sum((-1)^k/(2k+1),k,0,infinity)
Re,
voilà, j'ai retrouvé mon 676, youpi ! :-)
Ne connaissant pas grand chose au calcul formel, j'ai cherché dans la précision de SpeedCrunch, je l'ai mis sur automatique et voilà.
Je pense que la précision en automatique n'est pas fantastique mais je n'ai pas besoin de précision absolue. c'est pour écrire des expériences de pensées, et ça me permet, même donc, sans cette absolue précision, de visualiser un résultat et d'imaginer mon petit scénario.
Merci de votre aide.
À bientot.
voilà, j'ai retrouvé mon 676, youpi ! :-)
Ne connaissant pas grand chose au calcul formel, j'ai cherché dans la précision de SpeedCrunch, je l'ai mis sur automatique et voilà.
Je pense que la précision en automatique n'est pas fantastique mais je n'ai pas besoin de précision absolue. c'est pour écrire des expériences de pensées, et ça me permet, même donc, sans cette absolue précision, de visualiser un résultat et d'imaginer mon petit scénario.
Merci de votre aide.
À bientot.
