Utilisation du solveur excel
Résolu
mariam-j Messages postés 25 Date d'inscription Statut Membre Dernière intervention -
Bonjour,
Je souhaite utiliser le solveur pour répartir de manière optimale un ensemble de 600 objets classés en 4 caractéristiques qui les différencient, (a,b,c,d) dans une armoire de 20 tiroirs de capacités différentes (1,2,3,4) et de prestiges différents ( petit, moyen, grand - associé à la caractérisque d) et d'acceptation des caractéristiques différentes (a ou non-a). J'ai pour objectif l'optimisation, à la fois de répartition la plus totale des 600 objets de différente quantité (c) et le remplissage des tiroirs fonction de leur capacité, de leur prestige. Il s'agit d'un tirage sans remise. Pour autant les tiroirs vont de vider par les curieux qui viendront se servir, et il faudra bien penser à d'autres remplissage. C'est pour éviter les déceptions et les frustrations ;-) même si la curiosité est un vilain défaut...quoique.
Je pense au solveur car je crois qu'il permet d'utiliser des conditions pour appliquer les restrictions et obligations. Sauf que j'aurais bien besoin d'un coup de main pour le faire en étant guidé, aprés je ferai.
Une restriction sur la caractéristique (a : oui ou non), excluant 1 tiroir donné obligeant les 19 autres
Une obligation ensuite sur le remplissage des 20 tiroirs d'au moins un des 600 objets sur la base de leur caractéristique (b) et leur nombre (c) en fonction de la capacité du tiroir (1,2,3,4) et de la notion de prestige (petit - moyen - grand) caractérisé dans l'objet par (d)
Une optimisation pour faire en sorte que les tiroirs désignés soient rempli en fonction de leur capacité et de leur prestige...
Bien cordialement
Claude
Windows / Chrome 140.0.0.0
- Utilisation du solveur excel
- Liste déroulante excel - Guide
- Télécharger gratuitement notice d'utilisation - Guide
- Word et excel gratuit - Guide
- Si ou excel - Guide
- Déplacer colonne excel - Guide
4 réponses

Bonjour,
Un début de piste
Pour réaliser cette optimisation en utilisant un solveur, voici un guide étape par étape qui vous aidera à configurer le problème :
1. Modélisation des données
a. Définir les objets :
Chaque objet a 4 caractéristiques :
( a ) (oui ou non)
( b ) (caractéristique à considérer pour le remplissage)
( c ) (quantité d’objets de cette caractéristique)
( d ) (prestige : petit, moyen, grand)
b. Définir les tiroirs :
Chaque tiroir a :
Une capacité (1, 2, 3, ou 4)
Un prestige (petit, moyen, grand)
2. Création d’une feuille de calcul
a. Créer un tableau pour les objets :
Colonne 1 : ID de l’objet
Colonne 2 : ( a )
Colonne 3 : ( b )
Colonne 4 : ( c )
Colonne 5 : ( d )
b. Créer un tableau pour les tiroirs :
Colonne 1 : ID du tiroir
Colonne 2 : Capacité
Colonne 3 : Prestige
3. Définir les variables de décision
Créez une matrice (20 tiroirs × 600 objets) qui représentera combien de chaque objet est placé dans chaque tiroir. Par exemple, ( x_{ij} ) où ( i ) est un tiroir et ( j ) est un objet.
4. Ajouter les contraintes
a. Exclusion d’un tiroir basé sur la caractéristique a :
Si un tiroir est exclu, assurez-vous que pour ce tiroir, la somme des objets avec ( a = oui ) soit zéro.
b. Remplissage minimum des tiroirs :
Pour chaque tiroir, assurez-vous qu’au moins un objet avec la caractéristique ( b ) soit placé, en tenant compte de la capacité du tiroir.
c. Capacités :
La somme des objets placés dans chaque tiroir ne doit pas dépasser sa capacité :
[
\sum_{j} x_{ij} \leq \text{capacité du tiroir } i
]
d. Respect des caractéristiques :
Assurez-vous que chaque objet est placé selon ses caractéristiques, et respectez les conditions sur ( a ).
5. Fonction objectif
Définissez votre fonction objectif. Par exemple, vous pourriez vouloir maximiser le nombre total d’objets placés dans les tiroirs ou maximiser la valeur totale basée sur une mesure de prestige.
6. Utilisation du solveur
Une fois que vous avez configuré votre modèle dans une feuille de calcul (comme Excel), utilisez le solveur :
Définissez votre fonction objectif.
Ajoutez toutes les contraintes que vous avez définies.
Choisissez la méthode de résolution appropriée (par exemple, linéaire si toutes vos relations sont linéaires).
7. Analyse des résultats
Après avoir exécuté le solveur, analysez les résultats pour voir comment les objets sont répartis dans les tiroirs. Vous pouvez ensuite ajuster vos paramètres et répéter le processus si nécessaire.
8. Considérations supplémentaires
Pensez à planifier des réapprovisionnements en fonction des caractéristiques des objets qui sont souvent pris.
Évaluez la performance du système après un certain temps pour ajuster les stratégies de remplissage.

Bonjour,
Merci pour votre aimable aide, la capacité des tiroirs est explicitée, les objets sont de même nature. Imaginez une sphére pour un objet, un tiroir contenant x sphéres.
Par contre je rencontre un probléme technique que je vais illustrer...

J'ajoute que pour réduire la voilure, j'ai fait une tentative sur un échantillon représentatif de 392x13 soit 5096 variables. Premier jet, le solveur à répondu "trop de variables".
Alors prenant un angle de vue différent, ayant pré-rempli d'au moins 1 object chaque tiroir manuellement, je pars sur le cadrage vers une solution de remplissage de type chaque tiroir doit representer un % donné.Puisque le premier remplissage rend une équité de répartition soit un % represantant son total sur la somme des remplissages. Si je veux que tel tiroir représente + alors les autres devraient s'ajuster et le solveur fonctionner sur un ensemble fini...


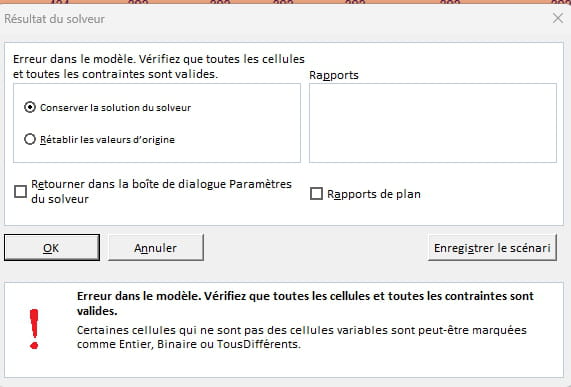

1000 mercis, je m'y colle de suite.
Alors : pour ma compréhension, "Créez une matrice (20 tiroirs × 600 objets) qui représentera combien de chaque objet est placé dans chaque tiroir" revient-il à créer une feuille avec les données, une colonne avec l'ID (j) objet et une ligne d'entête avec les ID (i) de tiroirs ?
Bonjour
Oui, c’est exactement ça ! Pour représenter une matrice de 20 tiroirs et 600 objets, vous pouvez créer une feuille de calcul où :
Ainsi, vous aurez une structure claire qui vous permettra de visualiser et de gérer facilement la distribution des objets dans les tiroirs. Les en-têtes de colonnes pourraient être les ID des objets et les en-têtes de lignes, les ID des tiroirs.