Calcul des termes d'une suite définie par récurrence
Bonjour,
J'ai un QCM de python à faire, mais j'ai beaucoup de mal. Serait-il possible qu'une personne m'aide à le résoudre ?
J'ai par exemple cette question :
Calculer le terme d'indice 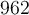 de la suite
de la suite 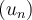 définie par :
définie par :
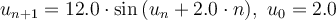 .
.
Vous donnez votre réponse comme un décimal avec au moins cinq chiffres significatifs.
Je ne vois pas qu'elle programme je peux faire ?
En vous remerciant.
- Calcul des termes d'une suite définie par récurrence
- Calcul km marche à pied gratuit - Télécharger - Sport
- Calcul moyenne excel - Guide
- Calcul charpente bois gratuit - Télécharger - Architecture & Déco
- Logiciel gratuit calcul valeur nutritionnelle - Télécharger - Santé & Bien-être
- Logiciel gratuit calcul surface m2 - Télécharger - Outils professionnels
5 réponses

Bonjour,
Mais Ducoup pour la question que j’ai posé sur les suites je ne vois pas dutout comment faire j’ai essayé de la faire mais je ne vois pas comment faire des suites en Python ?
Bonjour,
C'est pas Ducoup, c'est du coup :-)
Mais avant de la programmer en Python, est-ce que tu sais le faire sur le papier ?

Bonjour,
Peut-être devrais-tu commencer par chercher comment écrire une fonction récursive en python ? Et normalement la suite devrait être assez naturelle.
Pour rappel, la fonction sinus en python correspond à math.sin
from math import sin print(sin(0))
Bonne chance


u(n+1)=u(n)*(n+1)
u1=1
Je peux faire avec une fonction récursive, je préfère faire avec une boucle. Moins gourmand, et plus accessible pour un débutant.
def factrec(n):
if n<2:
return 1
else:
return n*factrec(n-1)
def factloop(n):
f=1
for i in range(2,n+1):
f=f*i
return f
print(factrec(5))
print (factloop(5))
Vous n’avez pas trouvé la réponse que vous recherchez ?
Posez votre questionJe suis d'accord avec yg_be.
Bien sûr, la solution récursive est plus élégante, mais la solution itérative est aussi simple dans le cas présent.
Le terme courant ne dépend que du terme précédent qui peut être accumulé dans une simple variable.
Même un problème comme la suite de Fibonacci se fait facilement en itératif.

