Courbe de tendance sigmoïde et Excel
Résolu
Audilala
Messages postés
11
Date d'inscription
Statut
Membre
Dernière intervention
-
Audilala Messages postés 11 Date d'inscription Statut Membre Dernière intervention -
Audilala Messages postés 11 Date d'inscription Statut Membre Dernière intervention -
A voir également:
- Excel sigmoid
- Liste déroulante excel - Guide
- Word et excel gratuit - Guide
- Déplacer colonne excel - Guide
- Si ou excel - Guide
- Excel moyenne - Guide
8 réponses
Je ne comprends pas : en insérant une courbe de tendance polynomiale de degré 2 directement sur le graphique de Audilala, j'obtiens une très jolie courbe en S ! https://www.cjoint.com/c/EHdq0hwzwdH
Cordialement.
Cordialement.
Bonjour,
et si tu nous mettais tes données et ta courbe attendue en pièce jointe !!!
tu peux le faire via cjoint ou équivalent.
cordialement
et si tu nous mettais tes données et ta courbe attendue en pièce jointe !!!
tu peux le faire via cjoint ou équivalent.
cordialement
Si les données ont une tendance linéaire, tu n'auras jamais une courbe de tendance parabolique ou sigmoïde !
Vous n’avez pas trouvé la réponse que vous recherchez ?
Posez votre question
Bonjour,
Tes données, c'est bien, mais ta sigmoïde, tu la vois où?
Ou plutôt, tu voudrais la voir où?
En effet, on peut toujours, moyennant changement de variable et jeux sur l'amplitude, trouver une sigmoïde qui fait la tendance de tes relevés (et même qui la fait mieux que la polynomiale de degré2).
Mieux que celle de degré 3, je n'ai pas trouvé (avec sigmoïde bien sur, sinon. en polynomial de degré supérieur, on améliore mais ça perds son sens).
Donc, il faut que tu en dises plus.
Tu peux toujours tester avec la fonction 83.50391/(1+EXP(-(x-14,891683)/12,456)) et comparer avec le polynôme de degré 2.
Sur [0, 100] tu arrives à retrouver la partie droite d'une sigmoïde.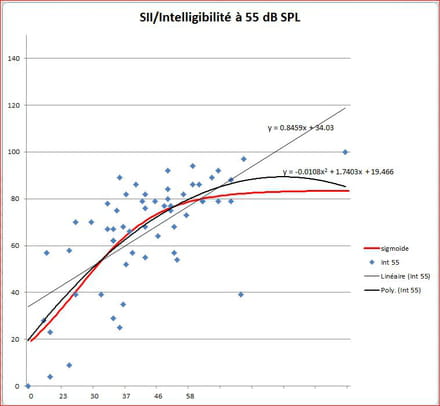
cordialement
Tes données, c'est bien, mais ta sigmoïde, tu la vois où?
Ou plutôt, tu voudrais la voir où?
En effet, on peut toujours, moyennant changement de variable et jeux sur l'amplitude, trouver une sigmoïde qui fait la tendance de tes relevés (et même qui la fait mieux que la polynomiale de degré2).
Mieux que celle de degré 3, je n'ai pas trouvé (avec sigmoïde bien sur, sinon. en polynomial de degré supérieur, on améliore mais ça perds son sens).
Donc, il faut que tu en dises plus.
Tu peux toujours tester avec la fonction 83.50391/(1+EXP(-(x-14,891683)/12,456)) et comparer avec le polynôme de degré 2.
Sur [0, 100] tu arrives à retrouver la partie droite d'une sigmoïde.
cordialement
Ah oui d'accord je ne voyais pas ce qu'il vous manquait..
Je cherche à obtenir une sigmoïde partant de (0;0) et allant à (1;1).
Je ne sait pas quel point de flexion elle aurait mais elle devrait ressembler aux courbes ci-dessous https://www.cjoint.com/c/EHdu21U2VGh
Ce serait à vérifier aussi mais elle pourrait suivre une équation du type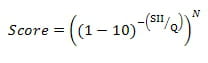
avec Q et N des variables à déterminer...
Merci pour tout !
Je cherche à obtenir une sigmoïde partant de (0;0) et allant à (1;1).
Je ne sait pas quel point de flexion elle aurait mais elle devrait ressembler aux courbes ci-dessous https://www.cjoint.com/c/EHdu21U2VGh
Ce serait à vérifier aussi mais elle pourrait suivre une équation du type
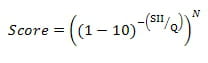
avec Q et N des variables à déterminer...
Merci pour tout !
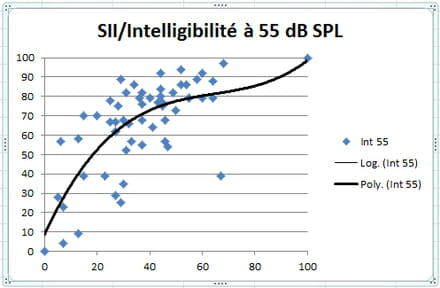
Et puis, c'est un S "à l'envers".
Mais ça correspond peut-être à la demande de Audilala
Cordialement
Et Audilala n'a pas précisé si le S devait avoir une position spéciale.
Celle-là me plaît bien : lascive, détendue, rebondie !
Amicalement.