Comment est générer la séquence avec srand ?
chaa13
-
KX Messages postés 16761 Date d'inscription Statut Modérateur Dernière intervention -
KX Messages postés 16761 Date d'inscription Statut Modérateur Dernière intervention -
Bonjour,
On sait que pour faire du pseudo-aléatoire il faut d'abord donner le premier chiffre de la séquence avec srand. Mais, a quoi ressemble cette séquence puisque seulement un chiffre sortira avec rand(), et comment la machine génère elle la séquence a partir du premier nombre (quel sont les opération quelle fait sur le premier nombre pour que les autres apparaissent)? Et comment fait il pour sortir le nombre a l'intervalle donnée ?
Ma question est peux être flou et j'en suis désoler.
Si quelqu'un peux m'éclairer ;)
Merci d'avance!
On sait que pour faire du pseudo-aléatoire il faut d'abord donner le premier chiffre de la séquence avec srand. Mais, a quoi ressemble cette séquence puisque seulement un chiffre sortira avec rand(), et comment la machine génère elle la séquence a partir du premier nombre (quel sont les opération quelle fait sur le premier nombre pour que les autres apparaissent)? Et comment fait il pour sortir le nombre a l'intervalle donnée ?
Ma question est peux être flou et j'en suis désoler.
Si quelqu'un peux m'éclairer ;)
Merci d'avance!
A voir également:
- Comment est générer la séquence avec srand ?
- Generer mot de passe - Télécharger - Sécurité
- Comment générer un qr code - Guide
- Comment couper une séquence vidéo - Guide
- Comment generer une table de matiere automatiquement - Guide
- Comment générer un tableau croisé dynamique - Guide
3 réponses
La génération de nombre aléatoires est une suite mathématique de type :
Voici une application logistique très simple qui permet de générer une suite infinie de nombres (sous réserve de bien choisir la première valeur de x).
Attention : c'est un exemple simpliste, la suite de nombres ainsi générée n'est pas équiprobable, on a plus de chance de tirer un nombre proche de 0 ou 1, qu'un nombre proche de 0.5
En pratique l'implémentation de générateurs pseudo-aléatoires utilisent une fonction plus sophistiquée qui rend la suite de nombre généré le plus équiprobable possible, mais on rentre dans des aspects assez poussé des mathématiques.
Au passage, j'explique le terme de "pseudo-aléatoire" : si tu connais l'algorithme utilisé et la valeur de la graine (la première valeur de la suite) alors tu peux calculer toutes les valeurs suivantes.
u[n+1] = f( u[n] )L'initialisation srand précise la valeur u[0] de la suite, et ensuite chaque appel à rand() va calculer u[n+1] en fonction de la valeur u[n] précédente.
Voici une application logistique très simple qui permet de générer une suite infinie de nombres (sous réserve de bien choisir la première valeur de x).
f(x) = 4x(1-x) avec x entre 0 et 1Par exemple en prenant x=0.3 comme première valeur, les 30 premières valeurs seraient :
0,3
0,84
0,5376
0,99434496
0,022492242
0,087945365
0,32084391
0,871612381
0,447616953
0,989024066
0,043421853
0,166145584
0,554164917
0,988264647
0,046390537
0,176953821
0,582564664
0,972732305
0,10609667
0,379360667
0,941784606
0,219305449
0,684842276
0,863333332
0,47195556
0,996854038
0,012544262
0,049547612
0,188370585
0,611548432
Attention : c'est un exemple simpliste, la suite de nombres ainsi générée n'est pas équiprobable, on a plus de chance de tirer un nombre proche de 0 ou 1, qu'un nombre proche de 0.5
En pratique l'implémentation de générateurs pseudo-aléatoires utilisent une fonction plus sophistiquée qui rend la suite de nombre généré le plus équiprobable possible, mais on rentre dans des aspects assez poussé des mathématiques.
Au passage, j'explique le terme de "pseudo-aléatoire" : si tu connais l'algorithme utilisé et la valeur de la graine (la première valeur de la suite) alors tu peux calculer toutes les valeurs suivantes.
Merci de t'a réponse !
Je crois que ça me fait penser a une certaine fonction qui si elle est mal choisi bloque tout les résultat (on as le même résultat tout le temps), je crois que cela avait un rapport sur un cours sur la théorie du chaos !
Mais le problème c'est comment la machine définie f(x) ? Comment fait-elle pour trouver une fonction approprié par rapport au f(0) pour que celle si soit toujours dans l'intervalle ?
Oui justement par rapport a la prévision des résultat, elle ne va pas pouvoir calculer indéfiniment les successions de résultats pour pour voir si sa fonction avec 0.3 en U0 respecte bien l'intervalle [0;1] !
Merci d'avance ;)
Je crois que ça me fait penser a une certaine fonction qui si elle est mal choisi bloque tout les résultat (on as le même résultat tout le temps), je crois que cela avait un rapport sur un cours sur la théorie du chaos !
Mais le problème c'est comment la machine définie f(x) ? Comment fait-elle pour trouver une fonction approprié par rapport au f(0) pour que celle si soit toujours dans l'intervalle ?
Oui justement par rapport a la prévision des résultat, elle ne va pas pouvoir calculer indéfiniment les successions de résultats pour pour voir si sa fonction avec 0.3 en U0 respecte bien l'intervalle [0;1] !
Merci d'avance ;)
"je crois que cela avait un rapport sur un cours sur la théorie du chaos"
Tout à fait, on a même les deux pieds dedans là !
Comment fait-elle pour trouver une fonction approprié par rapport au f(0) pour que celle si soit toujours dans l'intervalle ?
Ça c'est mathématiques, quand on sait que x est entre 0 et 1, on est sur que f(x) sera aussi entre 0 et 1, donc il n'y a pas de problème là dessus.
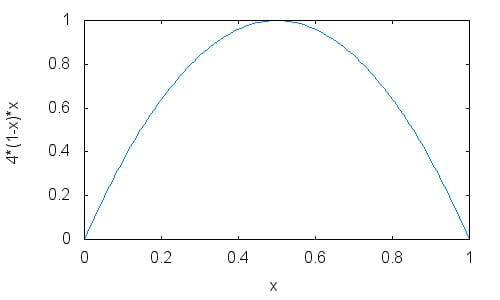
Par exemple en prenant 0.5 on va sur 1 puis 0, donc ça va pas.
Le problème c'est qu'il y a une infinité de valeurs qui feront converger vers 0, même si c'est une "petite infinité" comparé à l'infinité de valeurs u0 qui ne font pas converger vers 0...
De toute façon, cette application que j'ai donné n'est qu'un exemple, elle n'est pas utilisée comme générateur de nombre pseudo-aléatoire car la répartition des nombres n'est pas équiprobable !
Mais ce qu'il faut c'est comprendre le principe de ces suites, car même si la fonction sera plus ou moins sophistiquée pour permettre d'avoir toutes les propriétés que l'on veut, on se retrouvera avec le même raisonnement.
Sur internet j'ai trouvé un code pour la fonction rand en C, cela peut changer d'un compilateur à un autre, mais la fonction f est alors celle-ci :
Tout à fait, on a même les deux pieds dedans là !
Comment fait-elle pour trouver une fonction approprié par rapport au f(0) pour que celle si soit toujours dans l'intervalle ?
Ça c'est mathématiques, quand on sait que x est entre 0 et 1, on est sur que f(x) sera aussi entre 0 et 1, donc il n'y a pas de problème là dessus.
Par exemple en prenant 0.5 on va sur 1 puis 0, donc ça va pas.
Le problème c'est qu'il y a une infinité de valeurs qui feront converger vers 0, même si c'est une "petite infinité" comparé à l'infinité de valeurs u0 qui ne font pas converger vers 0...
De toute façon, cette application que j'ai donné n'est qu'un exemple, elle n'est pas utilisée comme générateur de nombre pseudo-aléatoire car la répartition des nombres n'est pas équiprobable !
Mais ce qu'il faut c'est comprendre le principe de ces suites, car même si la fonction sera plus ou moins sophistiquée pour permettre d'avoir toutes les propriétés que l'on veut, on se retrouvera avec le même raisonnement.
Sur internet j'ai trouvé un code pour la fonction rand en C, cela peut changer d'un compilateur à un autre, mais la fonction f est alors celle-ci :
f(n) = ((214013 * n + 2531011) >> 16) & 0x7FFFAvec n qui est de type long (donc on n'est plus entre 0 et 1 ici, mais sur tout l'intervalle des valeurs possibles).
