Les methodes pour convertir le nombre 4432 de base5 à base2
Utilisateur anonyme -
Bonjour,
comment convertir le nombre 4432 de base 5 à base binaire directement, sans passer de base 10 , mais en utilisant la méthode des divisions successives. Dans cet exemple la réponse est 1001101001 en base 2.
Windows / Chrome 117.0.0.0
- Rémi et safia ont découvert le code binaire
- Nombre de jours entre deux dates excel - Guide
- Telecharger macro convertir chiffre en lettre excel - Télécharger - Tableur
- Nombre facile - Télécharger - Outils professionnels
- Convertir epub en kindle - Guide
- Convertir kindle en epub - Guide
6 réponses

Salut,
pour moi, ce que j'en comprends, c'est qu'il faut faire ce qu'a indiqué Whismeril.
C'est-à-dire appliquer la méthode des divisions euclidiennes (qui marche quelle que soit la base) de manière informatique.
Ce qu'a indiqué PierrotLeFou est pour moi hors-sujet puisque la question ne porte pas sur la représentation interne mais plutôt sur des calculs mathématiques.

Bonjour,
Je ne suis pas assez bon en mathématiques pour apporter une solution.
Je pense cependant que lorsqu'on passe de la base 10 à une base n par des divisions successives, ces divisions sont faites avec les règles de calcul en base 10 telles qu'on les a apprises à l'école primaire.
Je suppose donc que si on veut passer de la base 5 à la base 2 par des divisions successives, il faudra utiliser de nouvelles règles de calcul pour faire ces divisions : des règles de calcul en base 5 qu'il reste à établir (tables de multiplication en base 5)
A priori, ça me semble pas du tout évident : il faudra apprendre à penser en base 5.
En cherchant un peu, je suis tombé sur cette page :
https://www.ilemaths.net/sujet-convertir-d-une-base-a-une-autre-sans-passer-par-la-base-10-450987.html
La technique est assez facile à comprendre.
Dans le cas d'un passage de la base 5 à la base 2, c'est abordable si on se limite à des petits nombres.
Mais ici, puisque arw a donné le résultat, on arrive à un nombre à 10 chiffres. Ce qui veut dire que dans les calculs on va monter jusqu'à 2^9 !
On commence à être dans des calculs énormes. J'ai regardé le début et j'ai laissé tomber.
Je suppose donc que si on veut passer de la base 5 à la base 2 par des divisions successives, il faudra utiliser de nouvelles règles de calcul pour faire ces divisions : des règles de calcul en base 5 qu'il reste à établir (tables de multiplication en base 5)
A priori, ça me semble pas du tout évident : il faudra apprendre à penser en base 5.
Oui, tel que je comprends la question, c'est exactement ça, d'où ma question de savoir si arw sait le faire à la main.
Parce que moi, non....
Additionner en base 5, je vais y arriver, par extension soustraire, mais multiplier ou diviser, là ça me dépasse.
Modération : tronqué car désobligeant
À partir de cette page https://tuto.pages-informatique.com/tables-division-base-5.php
J'ai défini que la table de division par 2 en base 5 est
0 / 2 = 0 reste 0
1 / 2 = 0 reste 1
2 / 2 = 1 reste 0
3 / 2 = 1 reste 1
4 / 2 = 2 reste 0
10/ 2 = 2 reste 1
11/ 2 = 3 reste 0
12/ 2 = 3 reste 1
13/ 2 = 4 reste 0
14/ 2 = 4 reste 1
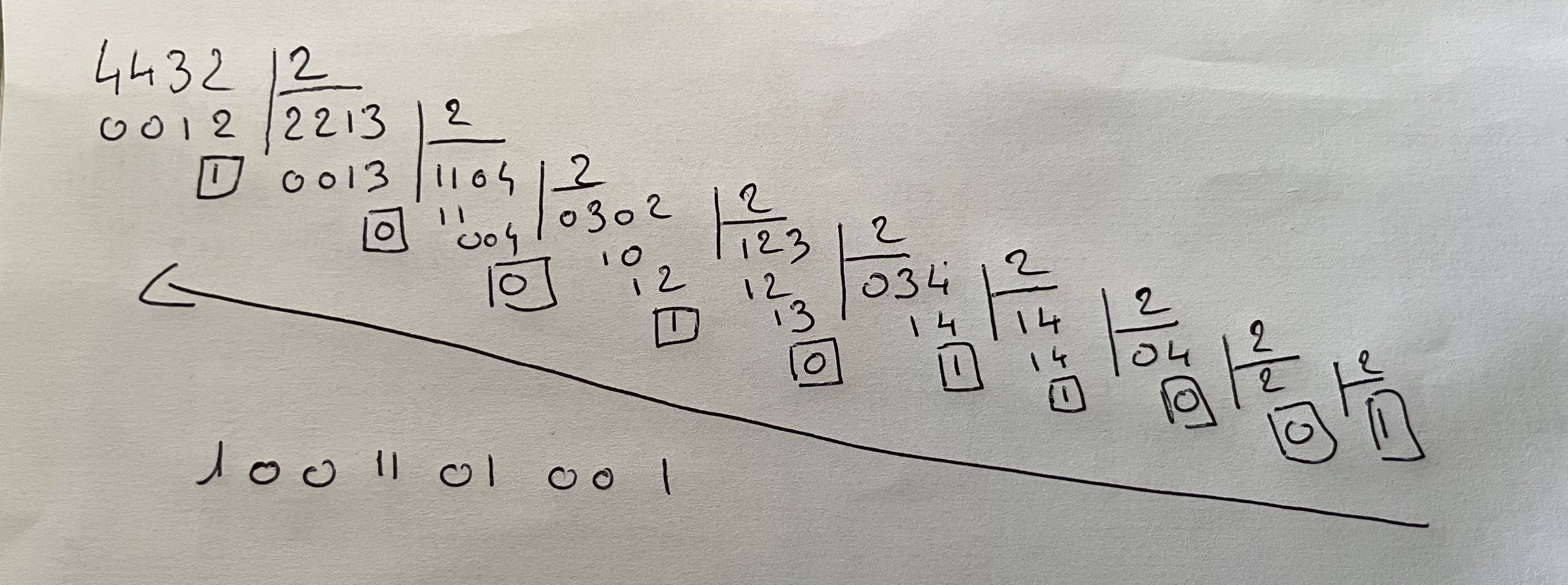
Et à partir cette table, finalement ce n'est pas si dur qu'il y parait, cf photo ci-dessus
J'ai vérité le résultat avec un convertisseur en ligne.
On peut donc écrire un algo en pseudo code qui arrive à ce résultat.
@arw je commencerai par une fonction qui prend un nombre de 1 ou 2 chiffres en entrée et retourne un tuple, un tableau, une liste, etc... de 2 valeurs, le quotient et le reste.

bonjour,
Pour moi, la réponse de PierrotLeFou est parfaitement appropriée.
Avant de faire des divisions successives par 2 afin de déterminer les chiffres du nombre en base 2, il faut enregistrer le nombre à partir de ses chiffres en base 5.
L'énoncé est particulièrement mal rédigé, et, comme les réponses proposées le prouvent, laisse la porte ouverte à de multiples interprétations.
Cela ne justifie nullement d'exprimer un avis négatif sur les interprétations des autres participants du forum.
Essayons de rester courtois, à défaut de réussir à être constructif.
Dans le code ci-dessous, il n'est fait nulle mention du système décimal ni des registres de la mémoire.
Je me fiche de la façon dont l'ordi fait ses calculs. Il sait comment les faire.
Je ne traite ni les nombres négatifs ni les erreurs.
Je ne fais aucune arithmétique simulée et je ne crois pas que c'est ce qu'on demande.
C'est trop compliqué pour un débutant.
def symbolic2numeric(symbol, base): # Conversion de la forme symbolique à la forme numérique.
b = len(base) # La valeur numérique de la base est le nombre de symboles dans la base.
number = 0 # Valeur de départ du nombre cherché.
for s in symbol: # On parcourt la liste des symboles.
# La position (ou index) est la valeur numérique associée au symbole à cette position.
digit = base.index(s) # Valeur numérique associée au symbole. Je suppose qu'il n'y a pas d'erreur.
number = number * b + digit # Je tasse le nombre d'une position et j'ajoute le digit suivant.
return number
def numeric2symbolic(number, base): # Convertion de la forme numérique à la forme symbolique.
b = len(base) # La valeur numérique de la base est le nombre de symboles dans la base.
symbol = "" # On commence avec une chaîne vide de symboles.
while number > 0: # Tant que le nombre est plus grand que 0.
s = base[number % b] # Symbole associé au chiffre des unités dans cette base.
symbol = s + symbol # J'ajoute le symbole à la gauche.
number = number // b # Je divise par la base pour obtenir la prochaine "colonne" en position des unités.
return symbol or base[0] # base[0] est le symbole associé au 0 dans cette base (requis si le nombre est 0 au départ)
nombre = symbolic2numeric("4432", "01234") # Je convertis "4432" en base 5 (5 symboles) vers la forme interne ou numérique.
symbole = numeric2symbolic(nombre, "01") # Je convertis ce nombre de la forme interne ou numérique vers la base 2 (2 symboles).
print(symbole) # J'affiche la valeur symbolique du nombre.

Bonjour,
Merci pour la proposition, mais comme le signalent blux et Whismeril, cette réponse ne répond pas aux contraintes de l'exercice. En effet, d'un point de vue maths :
- calculer number * b + digit revient à passer de la base b base 10 (ligne 7)
- calculer number // b et number % b revient à faire en passage de la base 10 vers la base b (ligne 14)
- il est dit explicitement dans l'énoncé qu'il faut faire des divisions successives par deux.
J'ai tronqué le fil de discussion en conséquence. Merci à chacun de rester courtois.

Bonjour,
Je pense qu'il est temps de mettre un terme à cette suite de propositions en tout genre et de ce concentrer uniquement sur la question du demandeur.
Encore une fois la question porte sur une conversion d'un chiffre en base 5 vers un chiffre en base 2 sans passer par la base 10 et en utilisant uniquement des divisions.
Pour l'instant, sauf erreur de ma part, une seule réponse allant dans ce sens a été proposée.
Vous n’avez pas trouvé la réponse que vous recherchez ?
Posez votre question
Finalement, c'est la question qui est hors sujet.
C'est un exercice de calcul écrit, décrit trop sommairement par arw, dans un forum inadéquat.
Ce qui explique que nos réponses ne conduisent pas un algorithme correspondant à l'énoncé.
Si la question avait été "comment faire une division écrite en base 5", nous aurions évidemment rapidement expliqué comment effectuer ce genre d'opération élémentaire.
Sans participation du demandeur, nous nous retrouvons souvent à batailler stérilement à propos de l'interprétation de la demande.
Bonjour à tous
Une autre idée sans passer par la base 10 : On compte de 1 à n en base 5 et en parallèle en base 2
https://www.cjoint.com/c/MJxqEW10ZLB
Cdlmnt